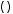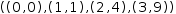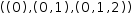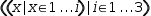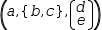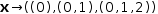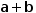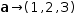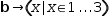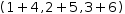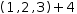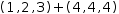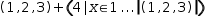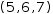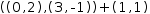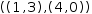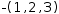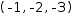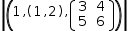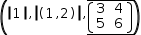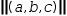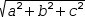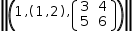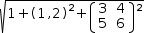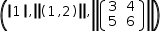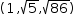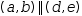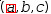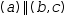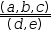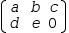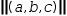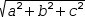6.2.1 Tuples
Mathematically, a
tuple
is an ordered list of elements.
In Myron, a tuple value is entered as a comma-separated list of
expressions delimited by parentheses. The displayed form is very
similar to the input form. For example, (1,3,5,7) represents both the
input syntax and the display of a tuple with 4 elements. However,
there is a minor variation in the input syntax of a single-element
tuple to distinguish it from a parenthesized subexpression. The
leading element of an entered tuple is allowed to be empty. Thus (6)
is a real subexpression while (,6) is a tuple with one element.
A tuple with 0 entries, called the empty
tuple, the 0-tuple or the null tuple, also uses the variation, being
entered as (,) and displayed as
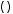 (, ).
(, ).
An element of a tuple may be any kind of expression. In particular it
may be another tuple element.
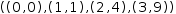 ((0, 0), (1, 1), (2, 4), (3, 9))
is a tuple of tuples (but note it is not a matrix). The constituent
elements need not be the same length nor even the same type.
((0, 0), (1, 1), (2, 4), (3, 9))
is a tuple of tuples (but note it is not a matrix). The constituent
elements need not be the same length nor even the same type.
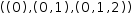 ((, 0), (0, 1), (0, 1, 2))
is a valid tuple with entries of different lengths. (In preview of
§6.3, this tuple can be generated by
((, 0), (0, 1), (0, 1, 2))
is a valid tuple with entries of different lengths. (In preview of
§6.3, this tuple can be generated by
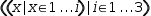 ((x|x∈1, i)|i∈1, 3).)
An example of a tuple with both different element lengths and different collection
types is
((x|x∈1, i)|i∈1, 3).)
An example of a tuple with both different element lengths and different collection
types is 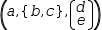 (a, {b, c}, [(, d), (, e)]).
(a, {b, c}, [(, d), (, e)]).
When all the elements of a tuple have the same type,
that type is called
the common type. If any element of a tuple
has a type different from any other element, the common type is said
to be indeterminate.
Tuples can be represented by variables.
A tuple variable is displayed as a simple variable in bold font, but
its input form has a different notation. To distinguish a tuple
variable from other variables, a tuple variable is decorated with the
type suffix t or ʈ [1].
A variable with a decoration like this is said to be explicitly typed.
A tuple can be bound to a variable by appearing in a definition in which
the variable appears on the defining side:
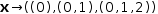 xʈ→((, 0), (0, 1), (0, 1, 2)). The variable does not need the ʈ decoration
in the input form
because the nature of the variable is inferred from the right side of
the definition. If, on the other hand, the variable on the defining
side does have a ʈ decoration, the elaboration must be a tuple expression.
As well, if the elaboration contains variables, a function will
be inferred for the left side.
xʈ→((, 0), (0, 1), (0, 1, 2)). The variable does not need the ʈ decoration
in the input form
because the nature of the variable is inferred from the right side of
the definition. If, on the other hand, the variable on the defining
side does have a ʈ decoration, the elaboration must be a tuple expression.
As well, if the elaboration contains variables, a function will
be inferred for the left side.
Tuples can also be associated with variables by appearing in an
equation in which one side is a simple variable name. Like
definitions, the types on each side of an equation must
match. Thus a variable on
one side of an equation is promoted to a tuple variable if the other side of
the equation is a tuple expression. At binding time,
the association implied by the equation is promoted to a definition.
To illustrate these points, consider the difference between the input
forms
(1,2)=x,
x→(3,4),
yʈ→(3,4)+(5,6)
and
yʈ=0. In the first two expressions, x is inferred to be a tuple variable.
The third expression indicates explicitly that y is a tuple variable.
The fourth expression is erroneous because the two sides of the definition
do not balance with respect to type.
In situations where there is no context that can be used to infer
a variable's type,
the variable must be entered using the explicit form.
To illustrate, an expression with explicit tuple variables entered as
aʈ+bʈ
displays as
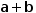 aʈ+bʈ.
In order for this expression to be
evaluated, definitions for a and b, like
aʈ+bʈ.
In order for this expression to be
evaluated, definitions for a and b, like
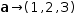 aʈ→(1, 2, 3)
and
aʈ→(1, 2, 3)
and
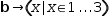 bʈ→(x|x∈1, 3)
must appear in the workspace.
Of course, incremental evaluation can always be performed by
selecting a variable and substituting. Contrast the tuple
expression above with an expression entered as
aʈ+b
and displayed as
bʈ→(x|x∈1, 3)
must appear in the workspace.
Of course, incremental evaluation can always be performed by
selecting a variable and substituting. Contrast the tuple
expression above with an expression entered as
aʈ+b
and displayed as
 aʈ+b. The latter case represents a mixed-type expression.
Binding for this expression would fail, as would an attempt to substitute,
because there is no definition for real b.
aʈ+b. The latter case represents a mixed-type expression.
Binding for this expression would fail, as would an attempt to substitute,
because there is no definition for real b.
When interacting with unary and binary operators, a tuple has primary
precedence. Any binary operators that can be applied to scalars can be
applied to two tuples or to a tuple and a non-tuple. In the case of two tuples
with the same number of elements, the operation is
applied to corresponding elements of each tuple.
For
example,
the expression  (1, 2, 3)+(4, 5, 6)
simplifies to
(1, 2, 3)+(4, 5, 6)
simplifies to
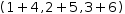 (1+4, 2+5, 3+6). If the tuples do not
have the same number of elements, residual elements from the longer
tuple are appended to the result unchanged. This is called the residual rule.
(1+4, 2+5, 3+6). If the tuples do not
have the same number of elements, residual elements from the longer
tuple are appended to the result unchanged. This is called the residual rule.
For binary expressions with a scalar as one
operand and a tuple as the other, the scalar operand is treated as if it
represented a tuple with the same number of elements as the
tuple operand, with each element being a copy of the scalar value (the scalar rule).
The mixed-type expression 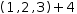 (1, 2, 3)+4
behaves like
(1, 2, 3)+4
behaves like
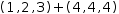 (1, 2, 3)+(4, 4, 4)
(and, more concisely, like
(1, 2, 3)+(4, 4, 4)
(and, more concisely, like
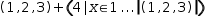 (1, 2, 3)+(4|x∈1, #(1, 2, 3))) and simplifies to
(1, 2, 3)+(4|x∈1, #(1, 2, 3))) and simplifies to
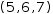 (5, 6, 7).
(5, 6, 7).
The rules for mixed-type binary expressions also consider nested tuples.
If one operand is a tuple of tuple of scalars and the other is a tuple of scalars,
both tuples of scalars are boxed.
Then the rules become the same as for binary expressions with
scalar and tuple,
this time with operands of type box and tuple of box (the box rule). Thus
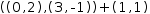 ((0, 2), (3, -1))+(1, 1) transform to
((0, 2), (3, -1))+(1, 1) transform to 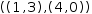 ((1, 3), (4, 0)).
((1, 3), (4, 0)).
The general case for mixed-type binary expressions follows
from the special cases described above.
If one operand is not a collection, the scalar rule applies.
If both operands are the same type of collection and one operand matches the common
type of the other,
the box rule applies;
if no such match can be made, the residual rule applies.
If the operands are collections with differing types,
the scalar rules applies with the operand of the "lesser" type taking the role of scalar.
The generalized rules are applied recursively until a situation
is reached in which the scalar rule can be applied.
Similarly, any unary operator that can be applied to scalars can be
applied to a tuple. For example,
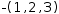 -(1, 2, 3)
simplifies to
-(1, 2, 3)
simplifies to
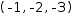 (, -1, -2, -3).
(, -1, -2, -3).
The cardinality of a tuple is produced by the unary operator #.
The operator
produces a real containing the number of elements in the tuple.
The input
#(1,(1,2),[(3,4),(5,6)])
displays as
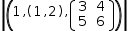 #(1, (1, 2), [(3, 4), (5, 6)])
and simplifies to 3.
Cardinality cannot be distributed but here is a situation
where Restructure applies; after restructuring, the expression appears as
#(1, (1, 2), [(3, 4), (5, 6)])
and simplifies to 3.
Cardinality cannot be distributed but here is a situation
where Restructure applies; after restructuring, the expression appears as
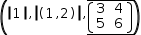 (, #1, #(1, 2), #[(3, 4), (5, 6)]) and
then simplifies to
(, #1, #(1, 2), #[(3, 4), (5, 6)]) and
then simplifies to
 ((, 1), (, 2), (2, 2)).
((, 1), (, 2), (2, 2)).
The magnitude of a tuple is given by the bifix unary | operator.
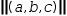 |(a, b, c)|
simplifies to
|(a, b, c)|
simplifies to
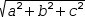 √(a^2+b^2+c^2).
√(a^2+b^2+c^2).
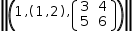 |(1, (1, 2), [(3, 4), (5, 6)])| is entered as |(1,(1,2),[(3,4),(5,6)])|.
Applied to the tuple, the operator evaluates the tuple's length as
|(1, (1, 2), [(3, 4), (5, 6)])| is entered as |(1,(1,2),[(3,4),(5,6)])|.
Applied to the tuple, the operator evaluates the tuple's length as 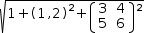 √(1+(1, 2)^2+[(3, 4), (5, 6)]^2).
The magnitude operator cannot be distributed but the expression can be restructured to
√(1+(1, 2)^2+[(3, 4), (5, 6)]^2).
The magnitude operator cannot be distributed but the expression can be restructured to
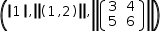 (, |1|, |(1, 2)|, |[(3, 4), (5, 6)]|).
This now simplifies to
(, |1|, |(1, 2)|, |[(3, 4), (5, 6)]|).
This now simplifies to 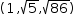 (1, √5, √86), with the first element being absolute value, the second
being vector length and the third being the sum of the squares of the elements of a matrix.
All, in a sense, mean magnitude.
(1, √5, √86), with the first element being absolute value, the second
being vector length and the third being the sum of the squares of the elements of a matrix.
All, in a sense, mean magnitude.
A tuple of scalars can be treated as a position vector (see §9.7 for a
better way to deal with vectors). Adding or
subtracting two position vectors produces a position vector.
Tuples of any length can by combined into a larger tuple using the
concatenation operator.
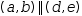 (a, b)‖(d, e)
simplifies to
(a, b)‖(d, e)
simplifies to
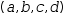 (a, b, c, d). The inverse occurs when the concatenation operator is introduced by
selecting and moving elements at either end of a tuple. That is,
(a, b, c, d). The inverse occurs when the concatenation operator is introduced by
selecting and moving elements at either end of a tuple. That is,
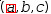 (.{a}, b, c)
and ← produce
(.{a}, b, c)
and ← produce
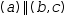 (, a)‖(b, c).
The horizontal concatenation operator combines tuples into a matrix by treating as rows.
(, a)‖(b, c).
The horizontal concatenation operator combines tuples into a matrix by treating as rows.
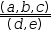 (a, b, c)‖‖(d, e) simplifies to
(a, b, c)‖‖(d, e) simplifies to 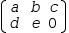 [(a, b, c), (d, e, 0)].
[(a, b, c), (d, e, 0)].
The length of a vector represented by a tuple is denoted
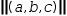 |(a, b, c)|. This simplifies to
|(a, b, c)|. This simplifies to
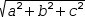 √(a^2+b^2+c^2).
√(a^2+b^2+c^2).